Linear Regression
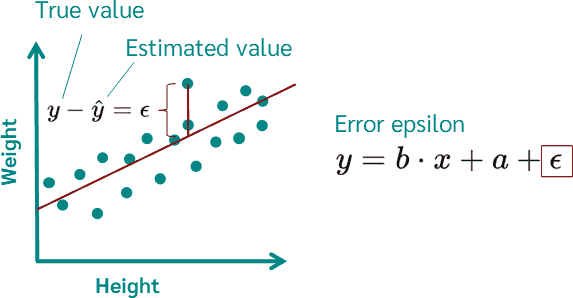
Linear Regression is a fundamental supervised learning approach for modeling the relationship between one or more explanatory variables (often called features or predictors) and a continuous target variable. The goal is to find a function (usually linear) that describes this relationship as accurately as possible.
Published on March 02, 2023 by Tung Nguyen
Machine Learning Probability and Statistics
3 min READ
Introduction to Linear Regression
Linear Regression is a fundamental supervised learning approach for modeling the relationship between one or more explanatory variables (often called features or predictors) and a continuous target variable. The goal is to find a function (usually linear) that describes this relationship as accurately as possible.
The simplest form, Simple Linear Regression, deals with one explanatory variable [ x ] and one response variable [ y ], aiming to fit a line:\
\[ y \approx \beta_0 + \beta_1 x. \]
More generally, Multiple Linear Regression deals with multiple features/predictors:
\[ \mathbf{y} \approx \mathbf{X}\boldsymbol{\beta}, \]
where
- [\mathbf{y} \in \mathbb{R}^n] is the vector of responses (target values),
- [\mathbf{X} \in \mathbb{R}^{n \times d}] is the design matrix (each row is a data point, each column is a feature),
- [\boldsymbol{\beta} \in \mathbb{R}^d] is the parameter vector we want to learn,
- [n] is the number of data points,
- [d] is the number of features.
Linear Regression Model
We assume a linear model of the form [ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}, ] where [\boldsymbol{\varepsilon}] is the noise or error term, often assumed to be normally distributed with mean 0 and variance [\sigma^2]: [ \boldsymbol{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \sigma^2 \mathbf{I}). ]
1. Maximum Likelihood Estimation (MLE)
Model Assumptions
- Each data point [ y_i ] is generated from a normal distribution:
\[ y_i \sim \mathcal{N}(\mathbf{x}_i^T \boldsymbol{\beta}, \sigma^2), \]
where [\mathbf{x}_i] is the [i]-th row of [\mathbf{X}].
- Hence, the joint probability of [\mathbf{y}] given [\boldsymbol{\beta}] and [\sigma^2] is:
\[ p(\mathbf{y} \mid \boldsymbol{\beta}, \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - \mathbf{x}_i^T\boldsymbol{\beta})^2}{2\sigma^2}\right). \]
Log-Likelihood Function
Maximizing the likelihood is equivalent to maximizing the log-likelihood:
\[\ell(\boldsymbol{\beta}, \sigma^2) = \ln p(\mathbf{y} \mid \boldsymbol{\beta}, \sigma^2)\]
\[= -\frac{n}{2}\ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n (y_i - \mathbf{x}_i^T\boldsymbol{\beta})^2.\]
We typically maximize [\ell] w.r.t. [\boldsymbol{\beta}] (and can separately solve for [\sigma^2]).
Maximizing w.r.t. [\boldsymbol{\beta}]
Ignoring terms that do not depend on [\boldsymbol{\beta}], we want to minimize:
\[\sum_{i=1}^n (y_i - \mathbf{x}_i^T\boldsymbol{\beta})^2 = (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^T(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}).\]
Taking the gradient of this quantity w.r.t. [\boldsymbol{\beta}] and setting it to zero:
\[ \frac{\partial}{\partial \boldsymbol{\beta}} (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^T(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) = -2 \mathbf{X}^T(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) = 0, \]
which yields
\[ \mathbf{X}^T \mathbf{X} \boldsymbol{\beta} = \mathbf{X}^T \mathbf{y}. \]
If [\mathbf{X}^T \mathbf{X}] is invertible (i.e., [\mathbf{X}] has full column rank), the MLE solution is:
\[ \boldsymbol{\hat{\beta}}_{\text{MLE}} = (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T \mathbf{y}. \]
Solving for [\sigma^2]
To find the MLE for [\sigma^2], substitute [\boldsymbol{\hat{\beta}}_{\text{MLE}}] into the log-likelihood and solve. The result is:
\[ \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n \bigl(y_i - \mathbf{x}_i^T \boldsymbol{\hat{\beta}}_{\text{MLE}}\bigr)^2. \]
(This could also be [\frac{1}{n-d}] if we use an unbiased sample estimator, but in standard MLE, we divide by [n].)
2. Ordinary Least Squares (OLS)
The Ordinary Least Squares approach seeks to minimize the sum of squared errors (residuals):
\[ \min_{\boldsymbol{\beta}} \; \sum_{i=1}^n (y_i - \mathbf{x}_i^T \boldsymbol{\beta})^2 = \min_{\boldsymbol{\beta}} \; (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^T(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}). \]
Following exactly the same derivation (taking the derivative w.r.t. [\boldsymbol{\beta}] and setting to zero), we arrive at the normal equations:
\[ \mathbf{X}^T \mathbf{X} \boldsymbol{\beta} = \mathbf{X}^T \mathbf{y}. \]
Thus, the solution is the same:
\[ \boldsymbol{\hat{\beta}}_{\text{OLS}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}. \]
Therefore, MLE (under the assumptions of normally distributed errors) and OLS yield the same parameter estimates.
Connection Between MLE and OLS
When we assume the errors [\boldsymbol{\varepsilon}] are i.i.d. Gaussian with zero mean and variance [\sigma^2], maximizing the likelihood is identical to minimizing the sum of squared residuals. Consequently, MLE and OLS solutions coincide.
Conclusion
- Linear Regression assumes a linear relationship between the predictors [\mathbf{X}] and the response [\mathbf{y}].
- Under Gaussian noise assumptions, the Maximum Likelihood Estimator of [\boldsymbol{\beta}] is the same as the Ordinary Least Squares solution.
- Both methods yield: [ \boldsymbol{\hat{\beta}} = (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T \mathbf{y}. ]